Risques sanitaires liés aux ondes électromagnétiques (OEM) - Notions fondamentales
La bonne compréhension et l'analyse critique des documents traitant des risques pour la santé consécutifs à l’irradiation par des rayonnements ou ondes électromagnétiques (OEM), nécessite l’assimilation de quelques notions fondamentales qui sont rappelées ici (les unités présentées font partie du SI -ou MKSA- adopté en 1946). Les notions présentées peuvent être précisées plus avant dans la page. Des explications plus détaillées peuvent être trouvées, par exemple, sur Wikipedia.
Sous-multiples et multiples utilisés
$$ \begin{align} f = femto &= 0,000\;000\;000\;000\;001 = 10^{-15} \\[6pt] p = pico &= 0,000\;000\;000\;001 = 10^{-12} \\[6pt] n = nano &= 0,000\;000\;001 = 10^{-9} \\[6pt] \mu = micro &= 0,000\;001 = 10^{-6} \\[6pt] m = milli &= 0,001 = 10^{-3} \\[6pt] k = kilo &= 1\;000 = 10^{3} \\[6pt] M = Mega &= 1\;000\;000 = 10^{6} \\[6pt] G = Giga &= 1\;000\;000\;000 = 10^{9} \\[6pt] T = Tera &= 1\;000\;000\;000\;000 = 10^{12} \\[6pt] P = Peta &= 1\;000\;000\;000\;000\;000 = 10^{15} \\[6pt] \end{align} $$
Rayonnements «ionisants» et «non ionisants» (RNI)
Les rayonnements électromagnétiques étudiés ici sont dits « non ionisants » par opposition aux rayonnements « ionisants ». Un rayonnement ionisant est un rayonnement qui produit des ionisations dans la matière qu'il traverse, c’est-à-dire que certains des atomes de cette matière vont être transformés en ions par arrachage ou ajout d’électron(s) dans ces atomes. Les rayonnements ionisants les plus connus sont les particules alpha (\( \alpha \)) et beta (\( \beta \)) ainsi que les rayons \( X \) et gamma (\( \gamma \)). Ils sont souvent associés à la radioactivité. La plus grande partie des rayons ultraviolets fait aussi partie de cette catégorie.
Rayonnements (ou ondes) électromagnétiques
Toutes les ondes (radio, TV, GSM, radars, micro-ondes, plaques de cuisson à induction…) mais aussi la lumière visible et invisible (infrarouge, ultraviolet, lasers) ainsi que les rayons \( X \) et \( \gamma \) sont des rayonnements (ou ondes) électromagnétiques. En physique des particules, toutes ces ondes sont associées à des photons, particule élémentaire de l’interaction électromagnétique qui appartient à la famille des bosons. Ces rayonnements électromagnétiques peuvent être ionisants ou non selon leur longueur d’onde (ou fréquence – voir ci-dessous) :
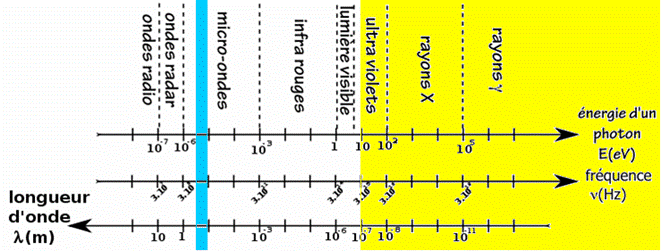
-
Les rayonnements électromagnétiques, dont la longueur d’onde est supérieure à 100 nm environ (fréquence inférieure à \( 3.10^{15} Hz\) i.e. 3 PHz, photons d’une énergie inférieure à 12 eV), sont considérés comme non ionisants (ceux étudiés ici entrent dans cette catégorie). A gauche et en blanc sur le dessin.
-
Les rayonnements électromagnétiques, dont la longueur d’onde est inférieure à 100 nm environ, sont considérés comme ionisants. Ces ondes correspondent à la plus grande partie du spectre du rayonnement ultraviolet, aux rayons \( X \) et aux rayons \( \gamma \). A droite et en jaune sur le dessin.
Les ondes étudiées ici (téléphones mobiles hors 5G, Bluetooth, WiFi, DECT), se situent dans la zone colorée en bleu (longueur d'onde comprise entre 12 cm et 33 cm).
La norme 5G de téléphonie mobile fait l'objet de chapitres séparés, clairement identifiés dans leurs titres.
NB : Dans les domaines de la photobiologie et de la photochimie, les rayons UV non ionisants sont classés en 4 catégories, selon leur longueur d'onde :
- UV-C : 100 nm à 280 nm,
- UV-B : 280 nm à 315 nm,
- UV-A1 : 315 nm à 340 nm,
- UV-A2 : 340 nm à 400 nm.
Au dessus de 400 nm de longueur d'onde, on trouve la lumière visible (400 à 780 nm), commençant par le violet
Au dessous de 100 nm de longueur d'onde, on trouve l'ultraviolet extrême (100 à 10 nm), qui est un rayonnement ionisant.
On sait depuis longtemps que les rayonnements ionisants sont potentiellement dangereux, voire mortels, pour les organismes vivants. On dispose, par contre, de très peu d’informations sur la dangerosité des rayonnements non ionisants.
Grandeurs physiques et unités employées pour caractériser les champs électrique et magnétique
Une OEM qui se propage dans l’espace engendre, dans celui-ci, un champ électrique (\( E \)) et un champ magnétique (\( H \)) qui sont liés et que l’on désigne par "champ électromagnétique". Du point de vue de la mécanique ondulatoire, les OEM sont décrites en détail par les équations de Maxwell. Toutes les normes officielles s'appliquant aux OEM étudiées ici sont exprimées dans le cadre de cette mécanique.
En pratique, dans les situations et les milieux qui font l’objet de la présente étude (champ libre ou tissus vivants), on verra que les différentes grandeurs physiques caractérisant les champs électromagnétiques sont liées et qu’il est facile de les comparer entre elles.
| Grandeurs physiques et symboles correspondants | Unités et symboles correspondants |
| Intensité du champ électrique (\( E \)) | volts par mètre (\( V/m \)) |
| (1) Champ d'aimantation ou champ d'excitation magnétique (\( H \)) | ampères par mètre (\( A/m \)) |
| (1) Champ d'induction magnétique (\( B \)) | teslas (\( T \)) (2) |
| Densité surfacique de puissance (S ou DSP) | watts par mètre carré (\( W/m^2 \)) |
(1) Pour comprendre la différence (subtile !) qui existe entre \( H \) et \( B \), il faut imaginer que \( H \) décrit l'excitation magnétique qui est, en quelque sorte, la cause.
Par contre, \( B \) décrit, au niveau local, l'"aimantation" propre de la matière sous l'effet d'une excitation magnétique externe qui lui est appliquée. C'est l'effet produit, sur le milieu étudié, de l'excitation appliquée. Celle-ci dépend bien sûr de l'intensité de la cause (\( H \)) mais aussi d'une propriété particulière du milieu : sa perméabilité magnétique \( \mu \).
L’intensité du champ d'excitation magnétique (\( H \) en \( A/m \)) et l’induction magnétique (\( B \) en teslas) sont liés par la relation suivante :
$$
B_{(T)} = \mu.H_{(A/m)}
$$
Avec \( \mu \) : constante de perméabilité magnétique du milieu étudié.
Dans le vide (ainsi que dans l’air et dans les matériaux biologiques avec une très bonne approximation), cette constante se nomme \( \mu_0 \) et vaut exactement \( 4.\pi.10^{-7}T.m/A \). A noter que \( \mu_0 \) est une constante de la physique.
Dans les situations qui font l’objet de la présente étude (champ libre ou tissus vivants), on a donc la relation de proportionnalité suivante :
$$
1 T = 4.\pi.10^{-7} A/m
$$
Ces deux grandeurs étant liées dans les situations qui font l’objet de la présente étude, on peut utiliser indifféremment l'une ou l'autre pour exprimer l'intensité d'un champ magnétique. L'habitude d'utiliser ( B ) en teslas s'est finalement généralisée.
(2) On rencontre encore parfois, dans certains anciens documents (bien qu’elle ne soit plus en vigueur depuis 1946 !…), l’ancienne unité (CGS) d’intensité du champ magnétique, le gauss (G ou Gs). Un gauss vaut simplement un dix millième de tesla :
$$ 1 G = 10^{-4} T $$ Pour des raisons de facilité de mesure, on relève plutôt la composante magnétique (en \( A/m \)) du champ électromagnétique des rayonnements basse fréquence, (fréquence inférieure à 10 kHz environ) et la composante électrique (en \( V/m \)) du champ électromagnétique des rayonnements haute fréquence, (fréquence supérieure à 10 kHz environ). Dans le cas d’une onde se propageant dans le vide ou dans l’air (cas qui nous intéresse ici), ces 2 grandeurs physiques sont liées entre elles : $$ E_{(V/m)} = Z0_{(\Omega)}.H_{(A/m)} $$ Z0, impédance caractéristique du vide, est une constante physique qui vaut environ 377 \(\Omega\). On a donc : $$ E_{(V/m)} = 377.H_{(A/m)} $$